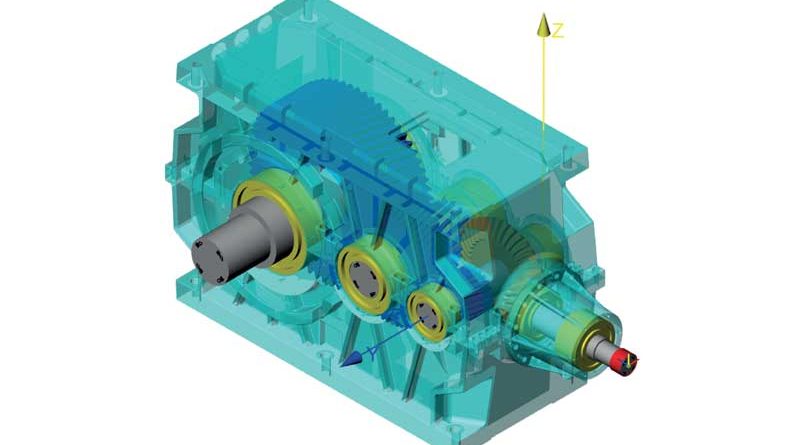
Come influisce la rigidezza della cassa del riduttore sul contatto delle ruote dentate

3 Settembre 2018 Giada Bianchessi 3056 Views KISSsoft

La rigidezza della cassa influenza la posizione dei cuscinetti e quindi l’allineamento degli alberi quando il riduttore è sotto carico. La deformazione della cassa non incide però direttamente sulle prestazioni degli ingranaggi, ma sono i disallineamenti degli alberi che si vengono a creare, le deformazioni degli alberi, dei cuscinetti e degli ingranaggi e le tolleranze di lavorazione a influenzare le condizioni di ingranamento. Questo studio mette a confronto tutti questi contributi per identificare quello più rilevante.

di Dipl.-Ing. Jürg Langhart, KISSsoft AG
di Dr.-Ing. Ioannis Zotos, KISSsoft AG
traduzione a cura dell’ing. Massimiliano Turci

La rigidezza della cassa di un riduttore influenza la posizione dei cuscinetti e quindi l’allineamento degli alberi quando il riduttore è sotto carico. La deformazione della cassa non incide però direttamente sulle prestazioni degli ingranaggi in termini di distribuzione del carico o di vibrazione. Sono i disallineamenti degli alberi causati dalla deformazione della cassa insieme alle deformazioni degli alberi, dei cuscinetti e degli ingranaggi e alle tolleranze di lavorazione a influenzare le condizioni di ingranamento. (*)

1. Esempio di applicazione
Si prenda in esame un riduttore ad assi ortogonali, attualmente in produzione alla Kissling AG in Svizzera. La potenza nominale è 600 kW e la temperatura di funzionamento varia fra 45°C e 60°C, con picchi fino a 80°C. Gli alberi e gli ingranaggi veloci possono lavorare a una temperatura leggermente più alta. La cassa è in ghisa EN-GJS 40.3 e presenta nervature di irrigidimento. Sono presenti uno stadio conico e dei due stadi ad assi paralleli.
Lo stadio conico ha un rapporto 17:37, la corona ha un diametro esterno di 460 mm ed è tagliata col procedimento Zyklo-Palloid®. L’albero pignone è supportato da una coppia di cuscinetti a rulli conici appaiati e da un cuscinetto orientabile a rulli.
Gli ingranaggi cilindrici sono elicoidali con modulo normale mn = 8 mm (coppia intermedia) e mn = 12 mm (coppia di uscita). Gli ingranaggi sono in acciaio cementato, rettificati con un grado di qualità almeno Q=6 secondo ISO 1328. Tutti gli altri alberi sono supportati da due cuscinetti orientabili a rulli.

2. Procedimento
L’obiettivo è identificare quali siano i contributi che incidono sulla richiesta di modifiche della microgeometria (spoglia di testa e bombatura più o meno asimmetrica) dei vari ingranaggi. Tali modifiche sono calcolate per via numerica con una LTCA (loaded tooth contact analysis, analisi di contatto sotto carico) come indicato nella ISO 6336-1, Annex E (calcolo della linea di contatto lungo la fascia)
Sono stati presi in considerazioni questi aspetti:
• Deformazione di alberi e cuscinetti (calcolo non lineare)
• Tolleranze di lavorazione di ingranaggi e cassa
• Deformazione della cassa
• Dilatazioni termiche a 80°C
Per calcolare la distribuzione di carico sugli ingranaggi come descritto nella ISO 6336-1 Annex E [1] e quindi l’errore di trasmissione è necessario un modello realistico delle deformazioni e dei cedimenti degli alberi. La componente assiale del disallineamento degli ingranaggi cilindrici non è importante come invece lo sono i cedimenti radiali H del pignone e J della corona conica. Per la coppia conica va posta particolare attenzione anche alle deformazioni termiche egli spostamenti assiali dei cuscinetti.

3. Esame degli stadi ad assi paralleli
3.1 Metodi per la valutazione dell’impronta di contatto
L’impronta di contatto va calcolata in due fasi. Prima di tutto va fatto il calcolo della distribuzione del carico lungo la fascia, poi quello della pressione di contatto fra i denti con la LTCA.
Per il calcolo della distribuzione del carico lungo la fascia è stato usato il metodo descritto nella ISO 6336-1 Annex E. Porta a risultati attendibili in tempi brevi e fornisce il valore del fattore KHβ necessario per il calcolo della capacità di carico degli ingranaggi. Questo metodo utilizza una LTCA monodimensionale la cui implementazione in KISSsoft è già stata descritta in [2].
È stato discusso nel comitato ISO-TC60 che si occupa della resistenza degli ingranaggi se vadano utilizzati i fattori di carico KA e dinamico KV nel calcolo della distribuzione di carico sulla linea. L’utente di KISSsoft può comunque scegliere come considerare questi fattori aggiuntivi nel calcolo del carico sulla linea [3].
È inoltre possibile fare un calcolo più raffinato con una LTCA bidimensionale, tenendo in considerazione il ricoprimento effettivo sotto carico [4]. Si ottengono risultati come l’errore di trasmissione, il conseguente PPTE, la potenza istantanea persa per attrito, la temperatura locale istantanea, lo spessore del film di lubrificante, il rischio a micropitting e così via. La LTCA bidimensionale porta a risultati molto più precisi rispetto al metodo della ISO 6336-1 Annex E, proprio perché quest’ultimo che considera invece solo il ricoprimento nominale.
È quindi ovvio che i due metodi portino a risultati diversi per la distribuzione del carico. Comunque, una volta che è stata applicata la necessaria modifica di microgeometria, le differenze sono davvero minime. È preferibile allora usare il primo metodo, che è più veloce, per calcolare la microgeometria e poi la LTCA bidimensionale per controllarne gli effetti (Figura 2).

3.2 Influenza della deformazione di alberi e cuscinetti
Di seguito è riportato lo studio dello stadio di uscita. Prima di tutto è stata calcolata la deformata dell’albero, che è funzione di taglio, torsione e flessione, con un metodo semi analitico basato sul modello di trave di Timoshenko.
Poi l’attenzione è stata posta sulla rigidezza non lineare dei cuscinetti, esaminando il contatto fra gli elementi volventi e le relative piste di rotolamento [5]. La compressione degli elementi volventi è il risultato dello spostamento relativo fra anello esterno ed interno.
Nel calcolo si è tenuto conto anche del gioco in esercizio, che dipende dal gioco interno iniziale del cuscinetto, dall’interferenza dell’accoppiamento con l’albero e l’alloggiamento, dalla dilatazione termica e dall’effetto centrifugo. In questa fase non è stata ancora presa in esame la deformazione della cassa.
Cioè l’anello esterno del cuscinetto è stato considerato ancora nella sua posizione teorica.
La proposta di modifica lungo la fascia è stata ricavata da KISSsoft basandosi sul già citato algoritmo della ISO 6336-1, Annex E. Per lo stadio di uscita, ad assi paralleli, è stata calcolata una bombatura asimmetrica composta da una correzione dell’elica cHβ = -11 μm e una bombatura cβ = 19 μm (Figura 3).
La Figura 4 mostra la distribuzione longitudinale del carico lungo la fascia wb con e senza la bombatura asimmetrica.
Il fattore di distribuzione longitudinale del carico KHβ passa da 1.17 (senza modifiche) a 1.01 (con la bombatura asimmetrica), confermando la bontà del valore suggerito da KISSsoft.

3.3 Influenza delle tolleranze di lavorazione
Oltre alla deformazione di alberi e cuscinetti, sono state prese in considerazione anche gli errori di lavorazione. Potrebbero essere proprio questi errori a determinare il disallineamento degli ingranaggi, quindi non possono essere trascurati nel definire le modifiche che li devono compensare. In genere si considerano due gruppi di tolleranze.
• Errore angolare di elica f Hb delle ruote
• Inclinazione dell’albero ed errori di disallineamento fSb, fSd
Gli errori di elica definiti nella ISO 1328 [6] sono collegati al grado di precisione (qualità) della ruota dentata e dipendono quindi dal processo di lavorazione (Figura 5). Nel caso in esame, per lo stadio di uscita, che ha un modulo normale mn=12 mm, il valore ammissibile dell’errore angolare dell’elica è fHb=15 μm per il pignone and fHb=16 μm per la corona. In KISSsoft, questi due valori possono essere considerati nel caso peggiore (con un disallineamento totale di 31 μm) oppure con approccio statistico (22 μm con una probabilità del 99.7%). Si è scelto quest’ultimo.
La ISO/TR 10064-3 [6] definisce le tolleranze per gli errori di posizionamento degli alberi, tenuto conto della larghezza di fascia delle dentature e delle distanze fra i cuscinetti. (Figura 6).
I valori ammissibili per questi errori sono funzione, della distanza fra i cuscinetti L, dell’errore totale di elica Fβ e della larghezza di fascia comune alle due dentature b, secondo queste relazioni:
I due contributi si combinano sul piano primitivo, dando un disallineamento totale, fΣ:

I valori di L, b ed Fβ sono stati ricavati dai disegni: gli errori di posizionamento degli alberi sono risultati fΣβ = 30 μm e fΣδ = 59 μm. Il disallineamento totale sul piano primitivo è quindi fΣ = 50 μm. Anziché usare questo valore, riferito al caso peggiore, si è preferito l’approccio statistico, con fΣ = 33 μm.
In alternativa si sarebbero potute considerare le tolleranze di posizione prese dalla tavola (Figure 7) o addirittura misurate i valori sulla cassa stessa.
Per compensare gli errori di costruzione, che hanno un orientamento casuale per loro natura, la correzione dell’angolo dell’elica non va bene. Va utilizzare la bombatura simmetrica o la spoglia di estremità (sempre simmetrica).
Per trovare il valore ideale di correzione dell’elica, si è utilizzato un algoritmo di ottimizzazione, combinando il valore costante di correzione dell’angolo dell’elica cHβ = -11 μm con quello di 10 possibili valori di bombatura, fra un minimo di 19 μm e un massimo di 55 μm (figura 8).
Per ciascuna della dieci proposte, oltre che per la situazione iniziale senza correzioni (indicata con 0), è stato calcolato il fattore di distribuzione longitudinale del carico KHβ, in modo da identificare quella che lo minimizza. La bombatura scelta è cHβ = 43 μm (Figura 9).
Successivamente è stato fatto un controllo globale incrociando tutte le combinazioni di disallineamento sul piano primitivo sulla linea d’azione fHb e di errori di costruzione fma (+fma +fHβ, +fma -fHβ, -fma +fHβ, -fma -fHβ).
La modifica scelta si è confermata quella ideale per compensare sia le deformazioni sia gli errori di costruzione che hanno un orientamento casuale. In tutte le condizioni è stato evitato il pericoloso contatto sulle estremità (Figura 10).
Si è concluso che le modifiche richieste sono cHβ = -11 μm e cHβ = 43 μm. In Figura 11, questi valori sono mostrati insieme alla bombatura di cHβ = 24 μm richiesta per compensare gli errori di costruzione. (figura 11). Il fattore di distribuzione longitudinale del carico KHβ varia così da 1.07 a 1.16, in funzione della combinazione degli errori di costruzione. Sono entrambi valori accettabili, il progetto è “robusto”, cioè è poco suscettibile alle variazioni nel campo delle tolleranze.

3.4 Influenza della deformazione della cassa
Come ultimo passaggio, è stata presa in considerazione la deformazione della cassa. La reazione del cuscinetto agisce come forza sulla cassa e la deforma, l’anello esterno del cuscinetto viene quindi riposizionato di conseguenza. La deformazione della cassa è calcolata direttamente da KISSsys utilizzando la matrice di rigidezza della cassa stessa condensata sui centri geometrici dei cuscinetti, sui quali sono applicate le reazioni dei cuscinetti come vettori forza. La matrice di rigidezza condensata può essere generata ed esportata dai più noti software FEM (ABAQUS, ANSYS or NASTRAN).
È necessario un calcolo iterativo [8], perché la deformazione della cassa influenza il calcolo dell’albero e quindi delle reazioni sui cuscinetti, che a loro volta deformano la cassa (Figure 12).

3.5 Particolarità della matrice di rigidezza
Nel modello FEM della cassa, il centro del cuscinetto è modellato con un singolo nodo, collegato alla sede tutt’attorno con elementi RBE2 or RBE3, a seconda del codice FEM usato. È una semplificazione accettabile, per quanto le forze assiali e radiali siano in realtà supportate da superfici differenti.
In figura 13 è mostrato l’albero intermedio, quello con le due ruote cilindriche. È supportato da cuscinetti orientabili a rulli. Sull’albero, in corrispondenza della sede dell’anello interno del cuscinetto, c’è una tolleranza p6; sulla cassa J6. La reazione assiale del cuscinetto si scarica sul coperchio e quindi passa alla cassa (percorso rosso), mentre quella radiale è supportata direttamente dalla cassa (percorso verde). Nel modello FEM, il cuscinetto orientabile a rulli è supportato invece da un’unica superficie, come se il modello fosse infinitamente rigido in direzione assiale. È un’approssimazione accettabile, in quanto lo spostamento assiale dell’albero non ha un effetto significativo sul contatto fra gli ingranaggi. La matrice di rigidezza condensata è importata in KISSsys e posiziona facendo coincidere i centri dei cuscinetti del modello KISSsys con i nodi posizionati nei centri dei cuscinetti del modello FEM. In seguito, col calcolo cinematico di KISSsys si ricavano le reazioni dei cuscinetti. Il vettore di tali forze di reazione, moltiplicato per la matrice di rigidezza, produce il vettore degli spostamenti dei cuscinetti (Figura 14). Prima di valutare l’influenza della rigidezza della cassa sul contatto fra gli ingranaggi, va notato che le deformate degli alberi, in particolare quelli degli alberi 3 (intermedio) e 4 (lento). La Figura 15 mostra lo spostamento radiale dei cuscinetti di questi due alberi considerando o no la rigidezza della cassa. In entrambi i casi sono stati stato presi in considerazione sia la deformazione sia il movimento dell’anello interno del cuscinetto rispetto a quello esterno, dovuto al gioco di funzionamento. La differenza di spostamento fra i due casi è meno di 10 μm (figura 15). Se è piccolo la differenza di spostamento degli alberi, considerando o no la rigidezza della cassa, sarà altrettanto piccola la differenza di modifica di elica necessaria per compensarla. Nel caso in esame. La differenza di modifica di elica è solo ΔcHβ = -2 μm: un valore che non ha significato fisico, visto che rintra all’interno delle tolleranze di lavorazione. Le modifiche di elica sono cHβ = -13 μm e cβ = 43 μm, Figure 16. In conclusione, si può affermare che la deformazione della cassa non ha influenza sul contatto nello stadio di uscita del riduttore in esame, per il quale la cassa è stata ben progettata ed è sufficientemente rigida.